지수의 비교 문제에 대한 생각

보통 다음 문제는 수학 문제의 흔한 유형이다.

$0 < b < a < 1$이라고 하자, 이때 $b^b,\,b^a,\,a^b$의 대소 관계를 비교하시오.

이런 문제는 보통 그래프를 그리면 쉽게 해결된다.

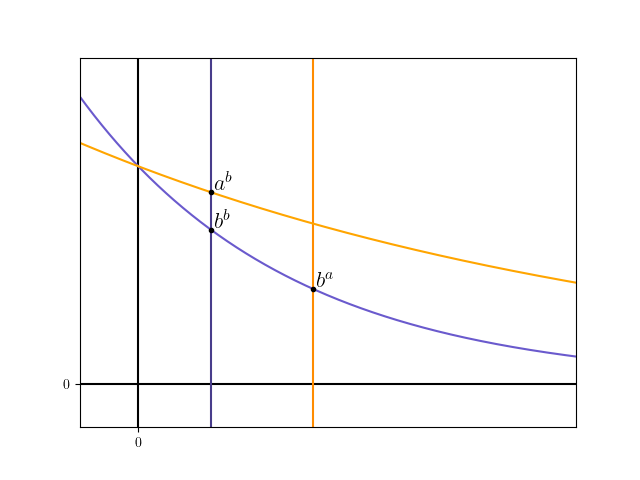
하지만 이 문제를 더 어렵게 만들려면 $a^a$를 추가하여 크기 비교를 하게 할 수 있었을 텐데 왜 그러지 않았을까?

그 이유를 살펴보기 전에 주어진 문제의 답을 구해보자.

위 그래프를 보면 문제의 답은 당연하게도 $ b^a<b^b<a^b $임을 쉽게 알 수 있다.

그렇다면 두번째 질문인 “왜 $a^a$를 추가하지 않을까”의 답을 알아보자.

이 질문의 답은 이 그래프를 또 보고 이해할 수도 있다.

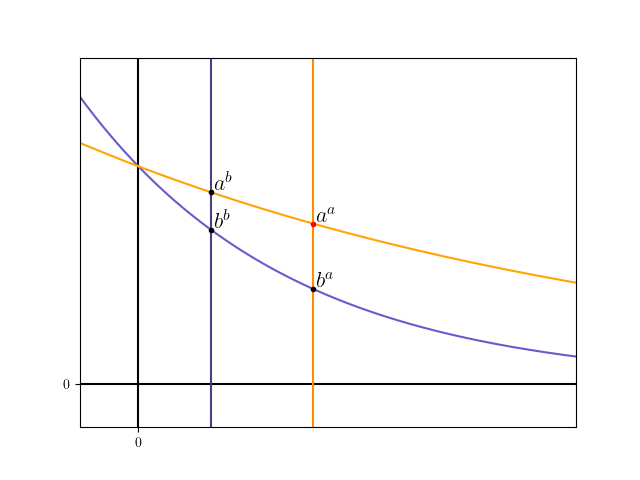
이 그래프를 보면 $a^a$와 $b^b$가 서로 확실한 대소관계를 가지는지 정확히 알 수 없을 것이다.

더 확실한 것은 다음 그래프와 위 그래프를 비교해보면 알 수 있다.

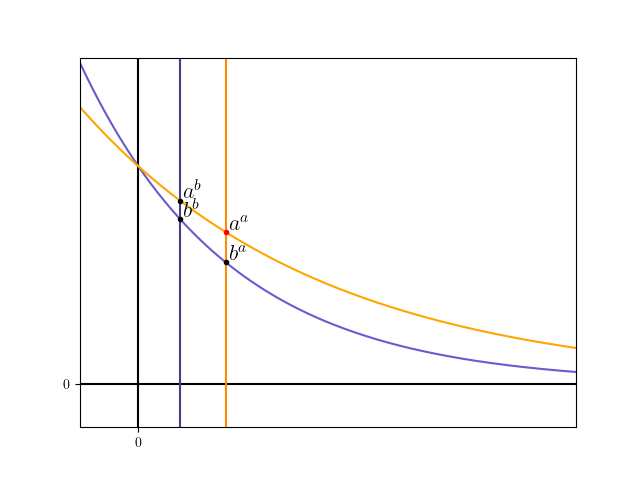
이같은 반례 때문에 문제에는 4가지 값이 한번에 나올 수 없다. 이로서 질문에 대한 답은 해결했다.

확장

하지만 이 더 나아가 “$a^a$와 $b^b$는 어느 점들을 경계로 서로 다른 크기를 가지게 되는가”같은 질문이 떠오르게 된다.

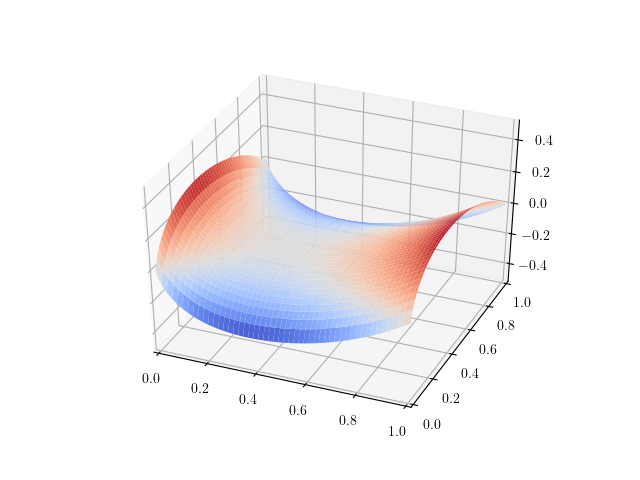
이 그래프는 $z=x^x-y^y$이다.

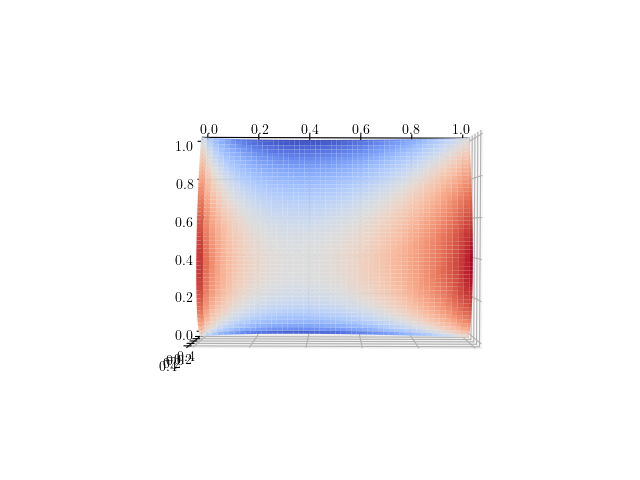
z축 방향에서 보면 더 명확하게 어디에서 경계가 형성되는지 알 수 있다.

이렇게 이 경계에 대해서는 알았지만 이 곡선이 무슨 곡선인지는 잘 모르겠다.