오일러 방법

근사적으로 미분 방정식을 푸는 방법으로 오차가 크게 난다.

\[x(t+h) \approx x(t) + h \times x'(t)\]

응용

위치 p의 업데이트는 속도 v에 대해 다음과 같이,

\[p = p + v\]

그리고 속도 v의 업데이트는 가속도 a에 대해 다음과 같이,

\[v = v + a\]

파이썬 구현

상황을 가정해보자 2초까지는 가속도 2로 움직이고, 2초부터 4초까지는 가속도 -2로 움직인다.

해석적 방법

이 방법으로 할 경우 속도 \(v(t) = \begin{cases} 2t & \text{ if $0\leq t < 2$} \\ -2t+8 & \text{ if $2 \leq t \leq 4$}\end{cases}\), 위치 \(p(t) = \begin{cases} t^{2} & \text{ if $0\leq t < 2$} \\ -t^2+8t-8 & \text{ if $2 \leq t \leq 4$}\end{cases}\)이다.

t = np.linspace(0, 4, 1000)

v = lambda _t: np.where(_t < 2, 2*t, -2*t+8)
x = lambda _t: np.where(_t < 2, 1/2*v(t)*t, -t**2+8*t-8)
plt.plot(t, v(t))
plt.plot(t, x(t))

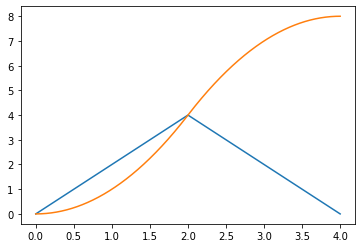어느정도 해석적인 방법

수치적 방법

위 오일러 방법을 이용해 적용해보면 다음과 같다.

t, dt = np.linspace(0, 4, 30, retstep=True)

# 초기값
a = lambda _t: 2 if _t < 2 else -2
v = [0] # v(0) = 0
x = [0] # x(0) = 0

for i, k in enumerate(t[:-1]):
    x.append(x[i]+dt*v[i])
    v.append(v[i]+dt*a(k))

plt.plot(t, v)
plt.plot(t, x)

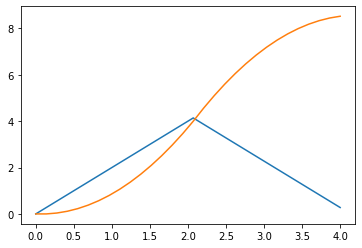
시간 간격이 더 작으면 작을수록 더 정확한 해가 나온다.