$log_x{a}$ 함수

별 생각 없이 생각해봤다. 학교에서 $\log_a{x}$만 주로 배우고 $\log_x{a}$는 배우지 않는다. 그 이유가 궁금해서 그래프를 그려보았다.

다음과 같이 $\log_x{a}$는 진수 조건에 의해 정의역 $\{x \vert x > 0, x \neq 1\}$을 가지는 $x\neq 1$에서 불연속인 그래프를 가진다.

사실 이 식 자체는 생각보다 흔히 볼 수 있는데, 그 이유는 밑변환 공식에 의해 이 식이 로그의 역수가 되기 때문이다.

\[\log_x{a}=\frac{\ln{a}}{\ln{x}}\]

이 함수의 미분

이 함수의 미분도 생각보다 간단하다.

\[\frac{d}{dx} {\log_x{a}}=\frac{\ln a}{x(\ln x)^2}\]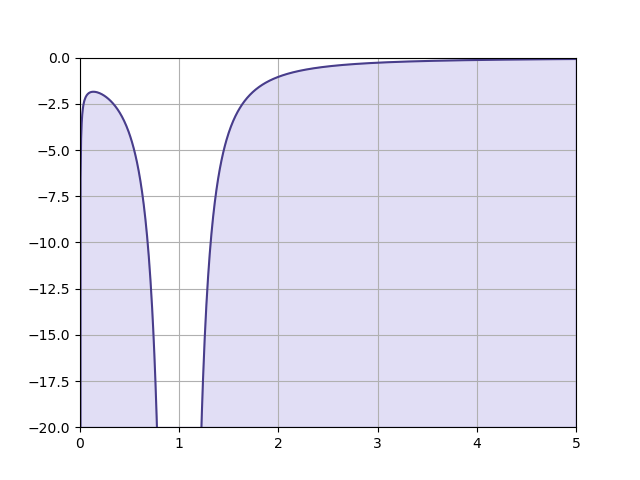

하지만 이로서 왜 이 함수를 안 다루는지 알 수 있을 것 같다.

이 함수의 적분

적분은 다음과 같다.

\[\int{\log_x{a}}=\ln a\int{\frac{1}{\ln x}}\]

이 식만 봤을 때는 의미가 없지만 로그 적분 함수의 정의를 생각해보면 그나마 의미가 있다.

\[\text{li}(x)=\int^{x}_{0}{\frac{dt}{\ln t}}\]

즉, 첫번째 식은 다음과 같이 쓸 수 있다.

\[\int{\log_x{a}}=\ln a \cdot \text{li}(x)\]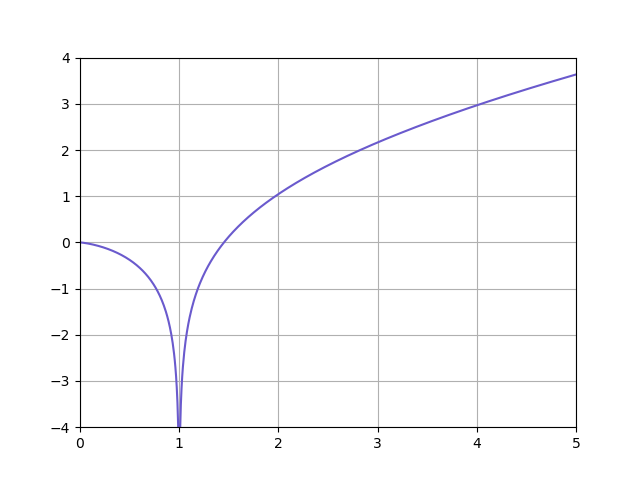

로그 적분 함수

로그 적분 함수를 처음 들은 것 같다. 로그 적분 함수는 물리학의 문제와 관련이 있고 정수론적 중요성을 지닌다고 한다. 특히 소수 정리는 소수 계량 함수 $\pi(x)$에 대해 다음을 보장한다고 한다.

\[\pi(x) \approx \text{li}(x)\]