접선이 만들지 못하는 도형

원의 모든 접선은 원 내부의 어떠한 점도 지나지 않는다.

사실 이 사실은 직관적으로 맞다는 것을 잘 알 수 있다. 그림을 보면 알 수 있다.

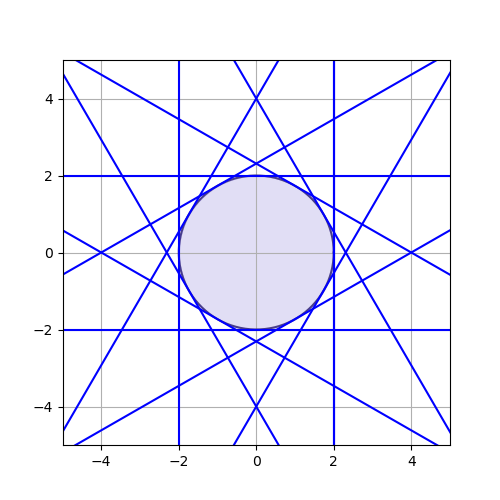
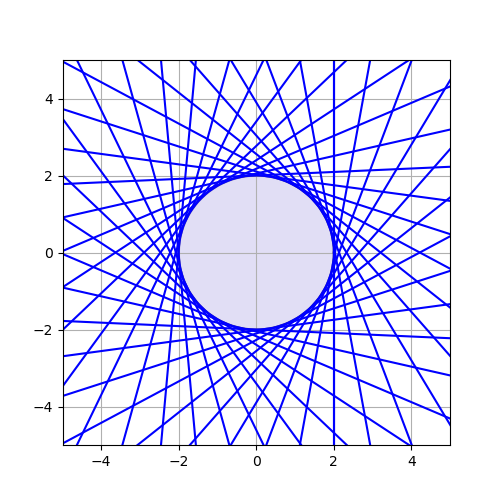
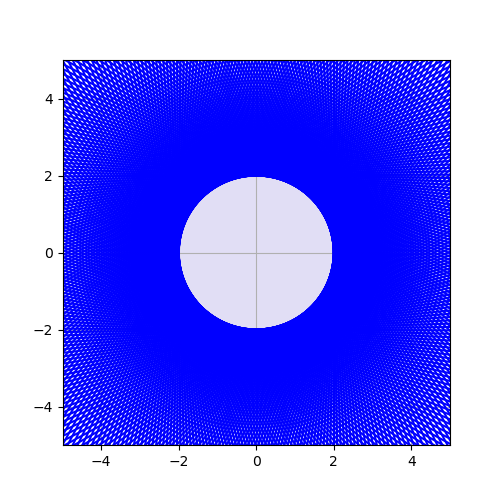
이는 비단 원 뿐만이 아니라 타원에서 성립한다.

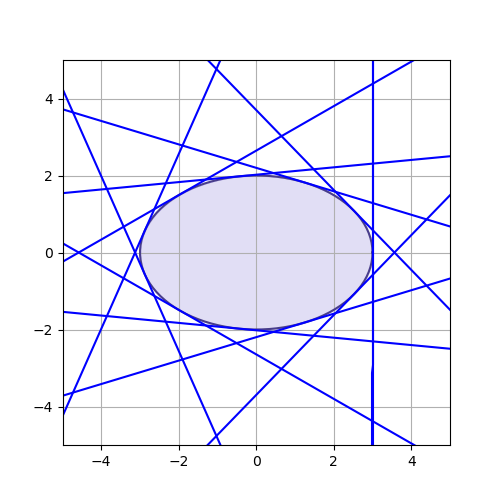
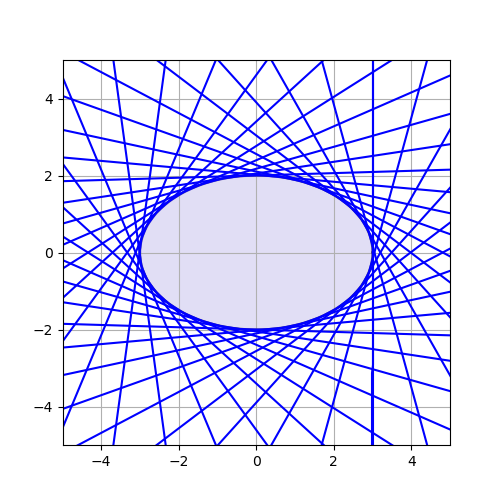
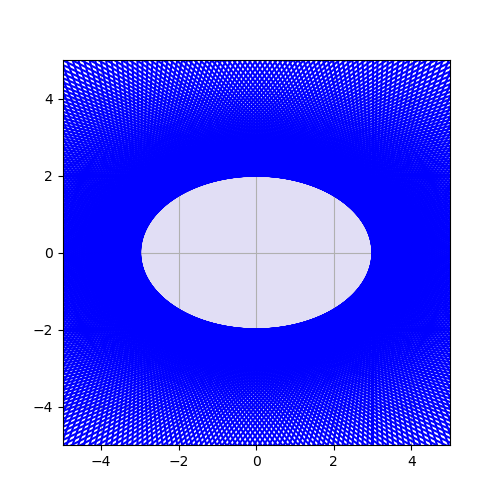
하지만 이것이 모든 점에서 접선이 존재하는 폐곡선에서 성립하지는 않는다는 걸 이 반례를 통해서 쉽게 알 수 있다.

\[x(t) = 2\sin{t} + \cos{t},\quad y(t)=2\cos(t)-\sin(2t)\]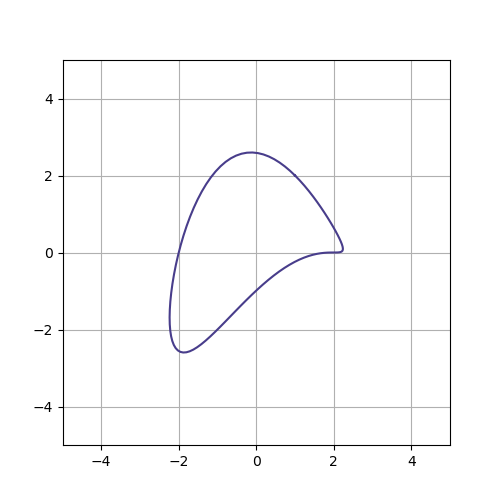

이 곡선이 왜 안되는지는 좀 그려보면 안다.

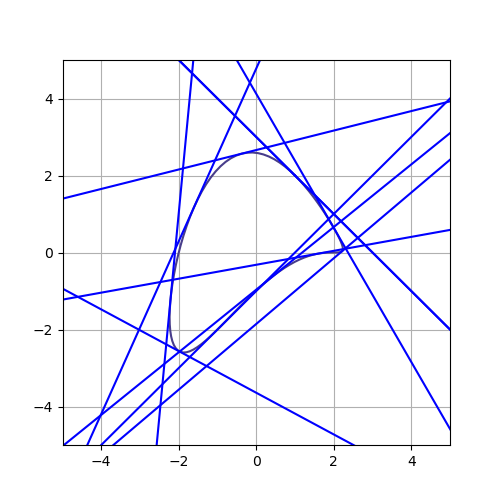
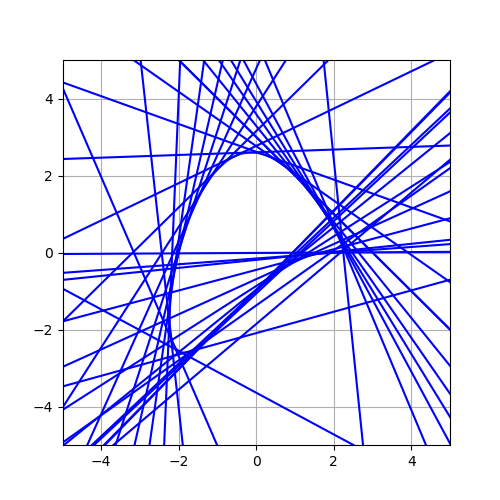
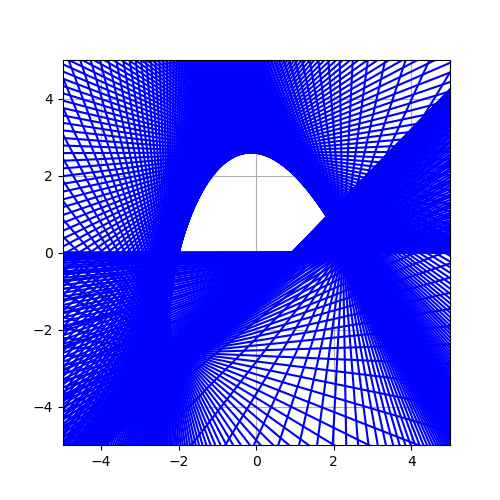
왜 이럴까? 나도 모르겠다.

좀 물어보니까 이것의 증명은 귀류법을 하면될 것 같기도 하다. 그냥 하면 된다.

그리고 이걸 확장시켜 볼록한 닫힌 도형에서는 그 접선이 내부를 관통하지 못한다고 추측할 수 있을 것 같다.

좀 함수적으로 생각해보면 모든 $x\in \mathbb{R}$에 대해$f’‘(x) > 0$ 혹은 $f’‘(x) < 0$이 성립하면 그 함수 내부점은 관통하지 못한다 할 수 있지 않을까?

원에서의 증명

원의 중심이 $(0, 0)$이고 반지름이 $k$인 어떤 원에 대해서 그 원 내부의 한 점 $P$와 원 위의 한 점 $Q$가 있다고 하자. 각각은 다음과 같이 나타낼 수 있다.

\[\begin{align*} P(x_1, y_1) &\quad x_1^2+y_1^2 < k^2 \\[1.25ex] Q(x_2, y_2) &\quad x_2^2+y_2^2 = k^2 \end{align*}\]

그리고 이는

\[x_1x_2 + y_1y_2=k^2\]

을 만족하는 $P(x_1, y_1)$은 존재하지 않는다.

라고 볼 수 있다.

이때 이 $P$, $Q$를 극좌표로서 다시 보면

\[\begin{align*} P(r_1, \theta_1) &\quad r_1 < k \\[1.25ex] Q(r_2, \theta_2) &\quad r_2 = k \end{align*}\]

\[r_1\cos{\theta_1}r_2\cos{\theta_2} + r_1\sin{\theta_1}r_2\sin{\theta_2}=k^2=r_2^2\]

을 만족하는 $P(r_1, \theta_1)$은 존재하지 않는다.

이는 다음과 같이 다시 쓸 수 있다.

\[\begin{align*} & \cos{\theta_1}\cos{\theta_2}+\sin{\theta_1}\sin{\theta_2} &= \frac{r_2}{r_1} \\[2ex] \Rightarrow\quad & \cos{(\theta_1-\theta_2)} &=\frac{r_2}{r_1}& \end{align*}\]

이때 $\frac{r_2}{r_1} > 1$, $-1 \leq \cos{(\theta_1-\theta_2)} \leq 1$ 이므로 조건을 만족하는 $P$는 존재하지 않는다.

볼록 함수

좀 도형에서 함수로 시점을 옮겨보자.

나는 이 관찰을 통해 볼록한 함수는 결코 접선이 그 볼록한 함수의 내부를 관통하지 못한다고 추측했다. (물론 내부는 볼록한 부분의 반대쪽이다.) 그렇다면 이 볼록함은 보통 2계 도함수 $f’‘(x)$를 주로 쓰니 이것을 활용해보면

모든 $x$에 대해 $f’‘(x) > 0$ 혹은 $f’‘(x) < 0$ 이면 함수 $f(x)$는 볼록하며 이 함수 $f$의 내부를 어떤 접선에 대해서도 관통하지 못한다

라고 추측 할 수 있다. 조금 조건부에서 느슨한 조건을 적용하면 2계 도함수 초과, 미만을 이상, 이하로 바꾸어 볼 수 있지 않을까 생각한다.

하지만 일반적인 함수는 이렇게 이상적으로 나오지 않는 경우가 많은데, 이 경우는 다음과 같이 정의할 수 있지 않을까 추측해본다.

구간 $(a, b)$에 대해 모든 $x\in(a, b)$가 $f’‘(x) > 0$ 혹은 $f’‘(x) < 0$이면 함수는 이 구간 내에서 볼록하며 이 구간 내의 함수 $f$를 이 구간 내에서 생성된 어떤 접선에 대해서도 관통하지 못한다.

라고 생각한다. 이또한 조건부에서 느슨한 조건의 적용이 가능할 것 같다.